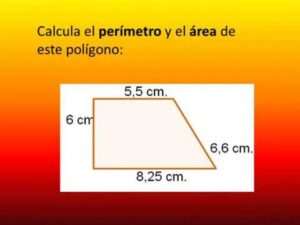
Cálculo del área de un trapecio irregular
El cálculo del área de un trapecio irregular es una tarea matemática que puede resultar desafiante para algunos estudiantes. Sin embargo, es una habilidad importante en la geometría y puede ser útil en muchas situaciones cotidianas, como la medición de terrenos o la construcción de edificios. En este artículo, se presentará una guía paso a paso para calcular el área de un trapecio irregular, así como algunos ejemplos de cómo aplicar esta habilidad en situaciones prácticas. También se discutirán algunas herramientas y fórmulas útiles que pueden facilitar la tarea. Con esta información, esperamos que los lectores puedan mejorar sus habilidades matemáticas y aplicarlas en su vida diaria.
Descubre la fórmula infalible para calcular el área de un trapecio escaleno
El cálculo del área de un trapecio irregular puede parecer complicado, pero con la fórmula adecuada, se puede hacer de manera sencilla y precisa. En este artículo, te enseñaremos cómo calcular el área de un trapecio escaleno utilizando una fórmula infalible.
¿Qué es un trapecio escaleno?
Un trapecio escaleno es un tipo de trapecio que tiene lados desiguales y dos ángulos opuestos que también son desiguales. Esto significa que las diagonales del trapecio no son iguales y que las bases no son paralelas.
La fórmula para calcular el área de un trapecio escaleno
La fórmula para calcular el área de un trapecio escaleno es:
A = ((b1 + b2) * h) / 2
donde:
- b1 y b2 son las bases del trapecio.
- h es la altura del trapecio, es decir, la distancia entre las dos bases.
- A es el área del trapecio.
Para utilizar esta fórmula, es importante conocer los valores de las bases y la altura del trapecio. Si no los conoces, tendrás que medirlos con una regla o una cinta métrica. Una vez que tienes estos valores, simplemente reemplaza los números en la fórmula y realiza los cálculos necesarios.
Ejemplo de cálculo del área de un trapecio escaleno
Imaginemos que tenemos un trapecio escaleno con las siguientes medidas:
- Base 1 (b1) = 8 cm
- Base 2 (b2) = 12 cm
- Altura (h) = 6 cm
Para calcular el área del trapecio, simplemente reemplazamos los valores en la fórmula:
A = ((8 + 12) * 6) / 2 = 60 cm²
Por lo tanto, el área de este trapecio escaleno es de 60 cm².
Descubre la cantidad de lados que tiene un trapecio irregular: guía completa
El cálculo del área de un trapecio irregular puede parecer complicado al principio, pero en realidad es bastante sencillo si conoces la cantidad de lados que tiene. En este artículo, te mostraremos una guía completa para que puedas descubrir la cantidad de lados que tiene un trapecio irregular y así poder calcular su área.
¿Qué es un trapecio irregular?
Antes de entrar en detalles sobre la cantidad de lados de un trapecio irregular, es importante entender qué es un trapecio irregular. Un trapecio es un polígono que tiene cuatro lados, dos de los cuales son paralelos y los otros dos no. Un trapecio irregular es aquel que no tiene sus lados paralelos iguales.
¿Cómo saber la cantidad de lados de un trapecio irregular?
Para saber la cantidad de lados de un trapecio irregular, necesitamos observar cuidadosamente su figura. Un trapecio irregular puede tener entre 4 y 6 lados, dependiendo de su forma. La manera más fácil de contar los lados de un trapecio irregular es dibujar una línea recta que una los dos lados paralelos y contar los lados que intersectan esta línea.
Por ejemplo, si dibujamos una línea que una los dos lados paralelos de un trapecio irregular y contamos que intersecta con otros 5 lados, entonces podemos concluir que este trapecio irregular tiene 6 lados en total.
¿Cómo calcular el área de un trapecio irregular?
Una vez que sabemos la cantidad de lados que tiene un trapecio irregular, podemos calcular su área utilizando la fórmula:
Área = (base mayor + base menor) x altura / 2
Donde la base mayor y la base menor son las medidas de los lados paralelos del trapecio, y la altura es la distancia entre estas dos bases.
Por ejemplo, si tenemos un trapecio irregular con una base mayor de 8 cm, una base menor de 6 cm y una altura de 4 cm, podemos calcular su área de la siguiente manera:
Área = (8 cm + 6 cm) x 4 cm / 2 = 28 cm²
Aprende fácilmente a calcular el área de un trapecio isósceles paso a paso
El cálculo del área de un trapecio irregular puede parecer difícil al principio, pero con estos simples pasos, podrás calcularlo fácilmente. En este artículo, nos enfocaremos en calcular el área de un trapecio isósceles, el cual tiene dos lados paralelos de igual longitud.
Paso 1: Identifica las medidas necesarias
Para calcular el área de un trapecio isósceles, necesitamos conocer la longitud de los dos lados paralelos y la altura del trapecio. Estas medidas se pueden encontrar en la figura del trapecio o se pueden medir directamente con una regla.
Etiquetaremos las medidas como a, b y h, donde a y b son las longitudes de los lados paralelos y h es la altura del trapecio.
Paso 2: Calcula el área
El área de un trapecio se puede calcular utilizando la siguiente fórmula:
Área = (a + b) × h ÷ 2
Para calcular el área de un trapecio isósceles, simplemente debemos reemplazar a y b con la longitud de los lados paralelos y h con la altura.
Área = (a + b) × h ÷ 2
Por lo tanto, el área del trapecio isósceles se puede encontrar multiplicando la suma de los lados paralelos por la altura y dividiendo el resultado por dos.
Paso 3: Ejemplo de cálculo del área de un trapecio isósceles
Imaginemos que tenemos un trapecio isósceles con lados paralelos de 8 cm y 12 cm y una altura de 6 cm. Para calcular el área, utilizamos la fórmula:
Área = (a + b) × h ÷ 2
Área = (8 + 12) × 6 ÷ 2
Área = 20 × 6 ÷ 2
Área = 60 cm²
Por lo tanto, el área del trapecio isósceles es de 60 cm².
Aprende a calcular el volumen de un trapecio paso a paso con ejemplos prácticos
El cálculo del volumen de un trapecio es una operación matemática esencial cuando se trata de la medición de objetos tridimensionales. Este proceso implica la multiplicación del área de la base del trapecio por su altura, lo que resulta en la obtención de su volumen.
Para calcular el volumen de un trapecio, lo primero que debemos hacer es determinar su área. La fórmula para calcular el área de un trapecio es:
Área = (Base mayor + Base menor) x Altura / 2
En esta fórmula, la base mayor y la base menor se refieren a los lados paralelos del trapecio, mientras que la altura se refiere a la distancia perpendicular entre estas dos bases.
Una vez que se ha calculado el área del trapecio, podemos proceder a calcular su volumen. La fórmula para calcular el volumen de un trapecio es:
Volumen = Área de la base x Altura
En esta fórmula, la «área de la base» se refiere al área que se ha calculado previamente mediante la fórmula del área del trapecio, mientras que la altura se refiere a la altura del trapecio.
Ahora, vamos a ver un ejemplo práctico para entender mejor cómo funciona este proceso:
Ejemplo: Imagina que tienes un trapecio cuya base mayor mide 8 metros, la base menor mide 6 metros y la altura es de 4 metros. Primero, debemos calcular el área del trapecio utilizando la fórmula:
Área = (8 + 6) x 4 / 2 = 28 metros cuadrados
Una vez que tenemos el área del trapecio, podemos calcular su volumen utilizando la fórmula:
Volumen = 28 metros cuadrados x 4 metros = 112 metros cúbicos
Por lo tanto, el volumen del trapecio es de 112 metros cúbicos.
Para calcular el área del trapecio, se utiliza la fórmula (Base mayor + Base menor) x Altura / 2. Una vez que se ha calculado el área, se utiliza la fórmula Volumen = Área de la base x Altura para calcular el volumen del trapecio.
En conclusión, el cálculo del área de un trapecio irregular puede parecer complicado al principio, pero con las herramientas adecuadas y un poco de paciencia, es posible obtener resultados precisos. Es importante recordar que cada trapecio irregular es único y debe ser abordado de manera individual. Por lo tanto, es fundamental comprender los conceptos básicos de geometría y aplicarlos correctamente para obtener una medida exacta del área. Esperamos que este artículo haya sido útil para comprender mejor el proceso de cálculo del área de un trapecio irregular.
En conclusión, el cálculo del área de un trapecio irregular puede resultar un poco más difícil que en el caso de un trapecio regular, ya que requiere la división del trapecio en diferentes triángulos y/o trapecios regulares para poder aplicar las fórmulas correspondientes. Sin embargo, con las herramientas adecuadas, como la geometría y el álgebra, podemos obtener una aproximación confiable del área de cualquier trapecio irregular que se nos presente. Es importante recordar que el cálculo del área es una habilidad fundamental en muchas áreas de la ciencia y la ingeniería, y que su aplicación práctica puede tener un impacto significativo en nuestra vida diaria.